The Chaos of the Sick Heart
By Jay A. Glasel, PH.D.
Managing Member
Global Scientific Consulting, LLC
A few years ago I attended a seminar on ventricular fibrillation (VF) research during which an eminent cardiologist made a remark that puzzled me. He said, "The more specific antiarrhythmic drugs become, the more dangerous they are." I was puzzled because I had always believed that, to avoid side effects, a drug should be highly specific for the macromolecular receptor it interacts with. And, of course, a large amount of drug research consists of finding the detailed structures of receptor binding sites so that drugs that can be designed to fit tightly and specifically into these binding sites.
One problem with VF is how to describe it accurately. That is, are the quivers of the heart muscle during VF random, or something else? The quivers in VF are caused by electrical activity in the heart that can be observed in an electrocardiogram. So we can ask if electrocardiogram patterns (millivolts [mV] vs time) can be interpreted as random.
Most of us are familiar with motions that vary regularly with time—for example, the oscillations of air that create a sound from a pipe organ. We can also hear sounds that occur at random—we call that noise.
But activity variations with time (such as cardiac electrical activity) are sometimes identified as random when they are actually “determined” variations. In the scientific sense, “determined,” means that the variations with time can be described exactly in an algebraic equation that can predict what the motions will be at a future time. Random variations don’t have this property—at any moment magnitude of the activity has no relation to what the magnitude will be at a succeeding time.
Chaos theory is a form of analysis deals with describing systems that have seemingly random properties but whose properties are actually determined. Chaos theory and the ways that chaos applies to biology has been the subject of a large number of publications in recent years including a best-selling popular book [2] and in reviews [3, 4].
Other than biology, the best known examples of chaotic systems are the weather and the economy. Both these systems are determinate in principle. Changes in the weather as time progresses should be mathematically predictable because the weather at any time depends on what it was at the preceding time. Nonetheless, in practice the weather is unpredictable because it is sensitive to the starting conditions of the analysis: We can't accurately describe the total state of the weather accurately enough at any given time to be able to make long range predictions of its future state. We can predict the short-term effects of a localized storm, but the same storm may set off a changed long-term weather pattern in a large volume of the atmosphere.
A key point in beginning to understand chaos theory is to understand that the way a chaotic system changes with time is highly dependent on its initial condition. We have all heard of the “butterfly effect” applied to the weather. As just mentioned, weather is chaotic and theoretically a butterfly flapping its wings somewhere in the world can result in a tornado somewhere else. Unfortunately, we do not yet have the equations that can accurately determine the connection between these two windy events.
It has been suggested that VF is a determinate phenomenon that looks random, but is actually chaotic [5] and that this may have important clinical/pharmaceutical implications.
A mathematical model suggested for VF [1] is a system where the electrical activity (as shown in an electrocardiogram), mVt, at a particular time, t, is given by Equation 1. In this model mVt is related to the electrical activity the system had at the preceding time, t-1, (mVt-1).
Equation 1. mVt = k(mVt-1)(1- mVt-1)
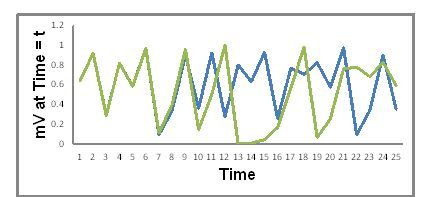
In Equation 1. k is a constant which in this illustration we will give a value of 4.000000. We will consider two initial conditions. The first initial condition is at t = 1, mV0 = 0.2000000. In the second initial condition, mV0 = 0.2000001. That is, the two initial conditions differ by only one part in a million from one another! Figure 1 shows a plot of the values of mVt vs t for this system under the two different initial conditions as calculated using Equation 1.
Figure 1. mVt vs time from equation 1 with two initial conditions. Blue = mV0 = 0.2000000; Green = mV0 = 0.2000001
Two things stand out in Figure 1. First, both plots look a lot like a random variation of mVt with time. Second, the blue and green variations of mVt with time begin to diverge a lot after t = 10 even though the initial conditions were only one part in a million different.
But in this illustration we know that mVt vs time is not random—it’s determined by equation 1. where at each time the value of mVt is determined by the value it had at the immediately preceding time (mVt-1)—our ideas of what is really random may need modification. We also see that as the system evolves with time how critically the values of mVt at later times depend on the starting values—this is an example of the butterfly effect.
Turning to the original point of this article, there is controversy concerning whether or not cardiac chaos is present in VF. The problem is distinguishing chaotic behavior from random fluctuations. That is: When the heart undergoes a transition from normal sinus rhythm to VF, do its motions become simply random (no relation between one quiver and the next), or are they chaotic (each quiver depends on previous ones in a determinate way such as in Equation 1)? There is evidence tending to support both models [1, 5] and the controversy Is ongoing.
Why should this seemingly esoteric point be important in considering the effects of antiarrhythmic drugs? Part of the answer is that if VF is a chaotic phenomenon, the specific action of a single drug may have unpredictable consequences on the whole heart much like the localized wind movement that can affect a large weather pattern—a cardiac butterfly effect.
This may underlie the fact that clinical antiarrhythmic drugs that block ion channels have not been effective in stopping VF and sudden cardiac death whereas drugs that block the general neurohumoral pathways that activate these channels (for example, beta blockers) are effective in saving lives. It is possible that in chaotic systems it's better to shut down or inhibit the whole system rather than tinkering with its parts.
Even more, it may be that the body in general needs to be considered as a chaotic system in the sense that, in some cases, perturbing one function by a drug may have widespread and unpredictable effects on general physiology.
References
1. Weiss, J.N., et al., Chaos and the transition to ventricular fibrillation: a new approach to antiarrhythmic drug evaluation. Circulation, 1999. 99(21): p. 2819-26.
2. Gleick, J., Chaos : making a new science. 20th anniversary ed. 2008, New York, N.Y.: Penguin Books. xiii, 360 p.
3. Crutchfield, J.P., et al., Chaos. Scientific American, 1986. 255: p. 46-57.
4. Rickles, D., P. Hawe, and A. Shiell, A simple guide to chaos and complexity. J Epidemiol Community Health, 2007. 61(11): p. 933-7. (can be downloaded from the Journal website)
5. Goldberger, A.L., et al., Nonlinear dynamics in sudden cardiac death syndrome: heartrate oscillations and bifurcations. Experientia, 1988. 44(11-12): p. 983-7.
Blog Categories
Stay Informed